La mujer con más alto IQ y el problema de Monty Hall 🎯
Tiempo de lectura: 4.63 minutos

Lo que encontrarás en este artículo
Es mucha coincidencia que el apellido de Marilyn vos Savant en francés signifique "erudito".
Siempre aprendió muy rápido, considerando su coeficiente intelectual de 228.
- Vos Savant nació en Estados Unidos, el 11 de agosto de 1946.
- Es hija de inmigrantes: su padre es alemán y su madre, italiana.
Sus padres nunca le dijeron que era excepcional.
Una vez dijo en una entrevista:
"Nadie realmente me prestaba mucha atención, sobre todo porque era mujer".
La persona más inteligente del mundo
El mundo le prestaría atención en 1985, cuando encabezó la lista del Libro Guinness de los Récords como la persona más inteligente del mundo.

Tenía casi 40 años cuando saltó a la fama.
Pregúntale a Marilyn
La revista Parade escribió sobre ella, y los lectores tenían tantas preguntas que la revista le ofreció una columna dominical, "Pregúntale a Marilyn" - que existe hasta el día de hoy.
En esa columna, se desató uno de los debates más acalorados sobre probabilidad del siglo XXI.

En 1990, un lector le hizo la siguiente pregunta:
- Imagina que estás en un concurso y te dan a elegir entre tres puertas.
- Detrás de una de ellas hay un coche, y detrás de las otras, cabras.
Eliges una puerta, digamos la número 1, y el presentador (que sabe qué hay detrás de cada puerta), abre otra puerta, digamos la número 3, te muestra que tiene una cabra y te pregunta:
"¿Quieres cambiar tu elección a la puerta número 2?".

¿Te conviene cambiar tu elección?
Esto se conoce como el problema de Monty Hall, nombrado así por el antiguo presentador del programa "Let's Make a Deal".

Te daré unos segundos para pensarlo.
La mayoría asume que ambas puertas tienen la misma probabilidad de contener el premio, por lo que no sienten necesidad de cambiar.
Sin embargo, Vos Savant respondió: "Sí, es mejor cambiar".
- La primera puerta tiene una probabilidad de 1 en 3 de ganar,
- pero la segunda tiene una probabilidad de 2 en 3.

Recibió muchas críticas por esta respuesta y no podía creer toda la reacción que generó.
Recibió miles de cartas de personas enfadadas, y el 90% de ellas decían que estaba equivocada.
Scott Smith, que tiene un PhD de la Universidad de Florida, escribió:
"Hay suficiente analfabetismo matemático en este país, y no necesitamos que la persona con el coeficiente intelectual más alto del mundo propague más. Vergonzoso".
Aquí hay una carta del profesor Robert Sachs de la Universidad George Mason:
"Te equivocaste. Como matemático profesional, me preocupa mucho la falta de habilidades matemáticas en el público en general. Por favor, ayuda confesando tu error y, en el futuro, siendo más cuidadosa".
Don Edwards, de Oregón, se expresó de esta manera:
"Quizás las mujeres ven los problemas matemáticos de manera diferente a los hombres".
Pero, en realidad:
Las personas que enviaron estas cartas poco amigables estaban absolutamente equivocadas.
Explicación del problema de Monty Hall
Cambiar de puerta aumenta tu probabilidad de ganar el premio.
A continuación, diversas explicaciones válidas.
Usando probabilidades
- Cuando eliges la puerta número 1, hay una probabilidad de 1 en 3 de que el premio esté detrás de esa puerta, y una probabilidad de 2 en 3 de que esté detrás de una de las otras dos puertas.
- Luego, el presentador interviene y te ayuda abriendo una puerta que sabe que no tiene el premio.
- Así, la puerta número 2 pasa a tener el resto de las probabilidades.
Pasó de tener una probabilidad de 1/3 a 2/3 de ganar el premio (ya que el presentador eliminó la puerta perdedora por ti).

Cambiar duplica tus posibilidades de ganar.
Analizando todas las combinaciones posibles
La protesta contra Vos Savant, fue tan extrema que se sintió obligada a dedicar varias columnas para explicar su lógica.
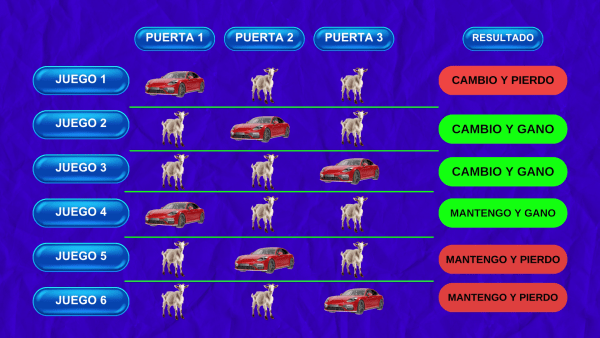
Demostró el beneficio de cambiar analizando los 6 escenarios posibles.
Para esto asumimos que el presentador siempre abre una puerta con una cabra.
Al mapear todas las posibilidades, se muestra que hay una mayor probabilidad de ganar si cambias que si te quedas con la misma puerta.
Exagerando el número de puertas
Es más fácil entender el problema si hay muchas más puertas.
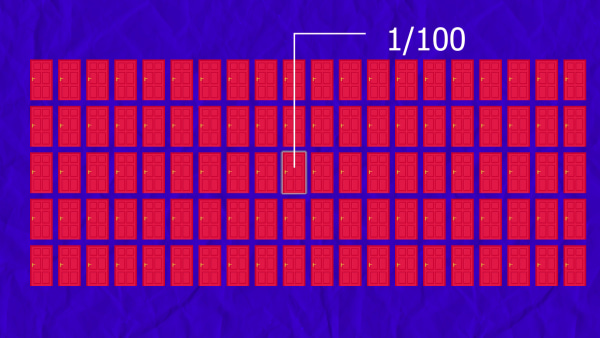
Imagina que eliges una puerta entre cien.
Luego, el presentador elimina 98 puertas que sabe que no tienen el premio detrás.
Quedan dos puertas, la que elegiste y la única otra que queda.
¿Cambiarías ahora?
Seguro que sí.
- Cuando elegiste al principio, solo tenías una probabilidad de 1 en 100 de haber elegido la puerta correcta.
- La probabilidad de que estuviera detrás de las otras puertas era 99/100.
- Luego, el presentador elimina 98 puertas incorrectas que sabe que no tienen el premio.
- Esto te favorece, porque esa probabilidad de 99/100 de tener el coche se ha resumido en la única puerta restante.
Admitieron su derrota
Muchos finalmente admitieron que estaban equivocados.
Un equipo del Instituto de Tecnología de Massachusetts (MIT) trabajó en el problema, y luego Seth Kalson, admitió:
"Tienes razón. Mis colegas en el trabajo se divirtieron mucho con este problema, y me atrevo a decir que la mayoría de ellos, incluyéndome a mí al principio, pensaron que estabas equivocada".
A lo que Marilyn respondió:
"Gracias, MIT, lo necesitaba".
En cuanto al profesor de matemáticas que vimos antes, el profesor Sachs, admitió:
"Después de quitarme el pie de la boca, ahora estoy comiendo un pastel de humildad. Como penitencia, responderé a todas las personas que me han escrito para castigarme. Ha sido una vergüenza profesional intensa.”
Simulación de 100 mil escenarios
Las explicaciones que vimos son muy buenas.
Pero, ¿te imaginas poder simular miles de escenarios en que el jugador a veces cambia de puerta, y a veces mantiene su decisión? Para ver si realmente, ¿conviene cambiar?
¡Eso es posible! ¡Y podemos hacerlo con la programación!
<!DOCTYPE html>
<html lang="es">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>Monty Hall</title>
</head>
<body>
<script>
function montyHall(switchDoor, trials = 100_000) {
let wins = 0;
for (let i = 0; i < trials; i++) {
// Configurar 3 puertas: dos cabras y un coche.
const doors = ['goat', 'goat', 'car'];
// Aplicar un orden aleatorio.
doors.sort(() => Math.random() - 0.5);
// El jugador elige una puerta aleatoriamente (0, 1, o 2).
let playerChoice = Math.floor(Math.random() * 3);
// Monty revela una puerta que el jugador no eligió y que tiene una cabra.
let montyChoice = null;
for (let j = 0; j < 3; j++) {
if (j !== playerChoice && doors[j] === 'goat') {
montyChoice = j;
break;
}
}
// Si el jugador opta por cambiar, elige la puerta que no fue elegida ni revelada.
if (switchDoor) {
for (let j = 0; j < 3; j++) {
if (j !== playerChoice && j !== montyChoice) {
playerChoice = j;
break;
}
}
}
// Si la elección final del jugador es el coche, contamos una victoria.
if (doors[playerChoice] === 'car') {
wins++;
}
}
const winPercentage = (wins / trials * 100).toFixed(2);
console.log(`Porcentaje de victorias cuando ${switchDoor ? "cambia de puerta" : "mantiene su elección"}: ${winPercentage}%`);
}
// Simulación:
montyHall(true); // 100 mil casos cambiando de puerta
montyHall(false); // 100 mil casos manteniendo su elección
</script>
</body>
</html>
Si no confiabas en las probabilidades, esta es la prueba definitiva.
Simulamos 100 mil casos en que el jugador cambia de elección, y 100 mil casos en que mantiene su elección.
Y como ves:
- ¡En promedio, el jugador ganó 66% o ⅔ de veces al cambiar de elección,
- y sólo 33% o ⅓ al mantener su elección!
Explicación en video
Por cierto, si quieres ver el video correspondiente a este tema, aquí lo tienes:
Aprende a programar
¿Te ha gustado la idea de simular miles de escenarios?
Si te gustaría aprender a programar, te invito a llevar mis cursos.
Con mis cursos te enseño a programar desde cero, y a crear tus primeras aplicaciones web y móviles.
Y si alguna vez tienes dudas, no te preocupes, siempre puedes consultarme y estaré encantado de ayudarte.
¡Gracias por leer hasta el final!